На пути своего развития и становления математическая логика встречала множество препятствий и проблем, которые не имели решения в определенный временной период. После неудачной попытки ввести в обиход проект Лейбница «Универсальная характеристика» прошло около полутора столетия, и только спустя это время была совершена еще одна попытка создать алгебру логики. Но надо отметить, что данная попытка имела новую основу, а именно концепцию множества истинности, что позволила сформировать математическую логику как теорию классов с множественно-теоретическими операциями. Лидерами в этой области деятельности были такие британские математики, как Джордж Буль и Август де Морган. Их вклад в развитие математической логики просто неоценим, благодаря им этот раздел сделал большой шаг вперед.
Шаг за шагом создавалась история
Август де Морган ввел в обиход символы для логических операторов и вскоре создал ныне известные «законы де Моргана». Немного позже он дал общее понятие математического отношения и операций над подобными отношениями.
Британский математик Джордж Буль абсолютно самостоятельно разработал свой вариант теории, который имел больший успех. В своих проектах с 1847 года по 1854 год он заложил основы современно математической логики, а также подробно описал алгебру логики. В результате таких действий появляются первые логические уравнения, а также входят понятия разложения логической формулы, то есть конституэнты.
Уникальная система Буля была усовершенствована Уильямом Стенли Джевонсом, который на основе работ Буля создал «логическую машину», способную легко решать логические задачи. В 1877 году Эрнест Шредер сформулировал сложный логический принцип двойственности. Немного позже Готлоб Фреге воспроизвел исчисление высказываний. А талантливый Чарльз Пирс в конце второй половины девятнадцатого столетия сформулировал общую теорию отношений и пропорциональных функций, а еще он ввел кванторы. Тот вариант символики, который мы видим и используем сегодня, предложил Пеано. После всех вышеперечисленных достижений и этапов развития математической логики все было готово для разработки в школе Гильберта теории доказательств.
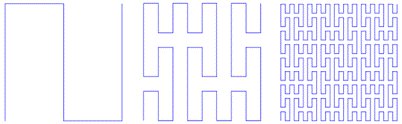
Кривая Пеано, первые три итерации
