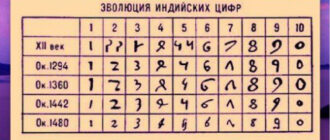
На формирование и дальнейшее развитие математики в странах ислама огромнейшее влияние оказала греческая и индийская научная традиция. Основываясь на опыте этих государств, исламские научные деятели развивали и усовершенствовали свои математические познания. Так, очень быстро получила большое распространение десятичная позиционная система исчисления с использованием нуля. Корни этой системы уходят в Индию. В эволюции математики как науки в странах ислама огромнейшую роль сыграли такие деятели, как Хорезми и Омар Хайям. Благодаря их научным работам исламская математика обрела статус самостоятельной дисциплины. К примеру, алгебраический трактат Хорезми гласит о классификации квадратных уравнений и содержит разнообразные приемы их решений. А вот трактат Омара Хайяма состоит из классификации кубических уравнений и непосредственно самой теории. Эти научные математические разработки стали основой для дальнейшего развития математики как самостоятельной дисциплины.
Математика ислама – усовершенствование классических приемов
Стоит сделать акцент на том, что математика Востока во все времена, в отличие от греческой, носила более практический характер. Поэтому неудивительно, что для исламских научных деятелей наибольшее значение имели измерительные и вычислительные аспекты. Основными сферами использования математики были строительство, торговля, астрономия, география, астрология, оптика и механика.
Исламские математики огромнейшее внимание уделяли геометрии и тригонометрии, а не только алгебре, что подтверждается большим количеством написанных работ на эти темы, дошедших до наших дней. Стоит отметить, что математики стран ислама «перевели» сферическую и плоскую тригонометрию из вспомогательного раздела астрономии в самостоятельную математическую дисциплину. Ранее же, к примеру, тригонометрия использовалась лишь для астрономических приложений. В своих трудах великие исламские математики осветили все 6 тригонометрических линий в круге, исследовали все случаи решения сферических треугольников, установили зависимость между тригонометрическими функциями, составили разнообразные тригонометрические таблицы, которые отличались высокой точностью, и вывели «бесценные» теоремы тригонометрии.
В целом, можно сделать вывод, что математики стран ислама чаще всего поднимали и усовершенствовали полуэмпирические разработки индийских научных деятелей на более высокую теоретическую ступень и тем самым повышали их уровень. И надо сказать, чаще всего на подобном синтезе все и заканчивалось; математики ислама дорабатывали старые разработки, практически виртуозно владели классическими методами, но в то же время большими успехами и новыми результатами похвастаться не могли.