Иерархическую классификацию Кантор рассматривал как продолжение порядка целых чисел. Таким образом, в математику была внедрена актуальная бесконечность – значение, которого математики прошлых лет всячески избегали.
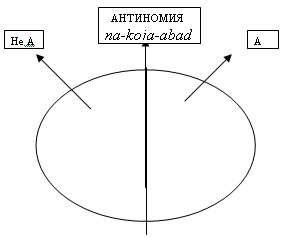
Противоречивые моменты теории множества
На первых этапах становления теория множеств была встречена математиками вполне одобрительно. Ведь она помогла обобщить жордановскую теорию меры, которая вполне успешно использовалась в теории интеграла Лебега. Стоит сказать, что теория множеств многими рассматривалась как твердая основа будущей аксиоматики всей математики. Но последующие события продемонстрировали, что привычная логика не подходит для исследования бесконечности, а интуиция не всегда бывает полезной в правильном выборе. Самое первое противоречие выявилось при рассмотрении самого большого множества, то есть множества всех множеств. Это произошло в 1895 году. В результате таких событий его пришлось исключить из всей математики как недопустимое. Но вскоре появились и другие противоречия, то есть антиномии.
Существует такой занимательный факт: Анри Пуанкаре, который изначально принял теорию множеств и даже очень часто использовал ее в своих разнообразных исследованиях, немного позже бесповоротно отверг ее и нарек «тяжелой болезнью математики». Но многие другие математики, к примеру, такие как Гильберт, Адамар и Бертран Рассел, не поддержали данное утверждение Пуанкаре и выступили в защиту «канторизма».
Такое положение значительно усугубило открытие «аксиомы выбора», которая, как позже оказалось, неосознанно использовалась во многих математических доказательствах, например в теории вещественных чисел. Данная аксиома объявляет этим множество, о составе которого ничего неизвестно, и это обстоятельство большая группа математиков посчитала исключительно неприемлемым, тем более что определенные следствия аксиомы выбора в корне противоречили интуиции.
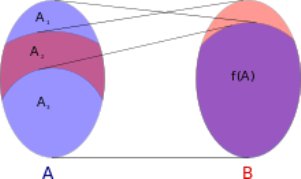
Схематическая идея доказательства теоремы Кантора — Бернштейна
В самом начале двадцатого столетия удалось согласовать вариант теории множеств без «примесей» ранних противоречий. Так что, большинство ученых того времени все же приняло теорию множеств. Но бывалого единства математики больше практически нет. Поэтому вовсе неудивительно, что некоторая часть научных школ стала формировать альтернативные взгляды на обоснование математики.